Рихвицкий В.С.  

• Поиск минимума с применением метода Ньютона

Поиск минимума с применением метода Ньютона

> with(linalg): with(plots): with(codegen): currentdir(`c:/rqvtsk/test`);

     Это демонстрационный пример автоматического построения
вычислительой программы на Паскале.
>  Пусть ищется минимум функции двух переменных

                            F:=subs(x=x+1,y=y+1,(A*arcsin(x)^2+B*arcsin(y)^2));

      зависящей от переменных

                            V:=[x,y];

>   Это график функции:

              plot3d(subs(A=1,B=1,F),x=-3.1..1.1,y=-3.1..1.1,axes=boxed,orientation=[145,82]);

>  Условием минимума является равенство нулю градиента функции

                G:=grad(F,V);

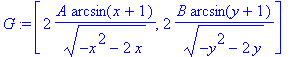
>  Метод решения (уже на Паскале) содержит итерацию

                                     V = V - H^(-1) G

                H:=hessian(F,V);

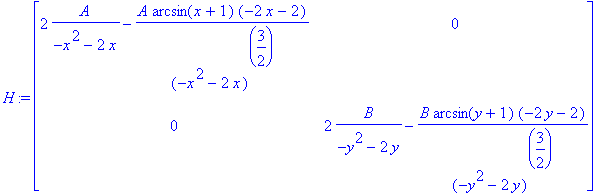
>   Для реализации программы на Паскале изготавливаются сначала процедуры
  (в Maple)

           GProc:=makevoid(makeproc(G,parameters=V,globals=[A,B]));

>  и

            HProc:=makevoid(makeproc(H,parameters=V,globals=[A,B]));

>   Затем они записываются в файл test2.txt на языке C

     writeto(`test2.txt`):
        C(GProc,optimized);
        C(HProc,optimized);
     writeto(terminal);

>   и перерабатываются в модуль test2.pas на Паскале
    (который, быть может использует модуль test1.pas)

          system(`c2pas test2(test1)`);

>    Главная программа test.pas и модуль test1.pas пишутся
 программистом и содержат все, что программист пожелал
 сделать традиционным путем.
    Далее программа обычным путем транслируется, выполняется
 и получается результат,
 который в данном случае мог быть получен аналитически:

            {solve(convert(subs(A=1,B=1,G),set),{x,y})};

>